METODE TRANSPORTASI
Dilihat dari namanya, metode transportasi digunakan untuk mengoptimalkan biaya pengangkutan (transportasi) komoditas tunggal dari berbagai daerah sumber menuju berbagai daerah tujuan. Tiga hal penting harus diingat dari penjelasan di atas, yaitu komoditas tunggal, daerah sumber (asal) lebih dari satu dan daerah tujuan juga lebih dari satu.
Meskipun demikian, metode transportasi tidak hanya berguna untuk optimasi pengangkutan komoditas (barang) dari daerah sumber menuju daerah tujuan. Metode transportasi juga dapat digunakan untuk perencanaan produksi. Data yang dibutuhkan dalam metode transportasi adalah:
1. Level suplai pada setiap daerah sumber dan level permintaan pada setiap daerah tujuan untuk kasus pendistribusian barang; jumlah produksi dan jumlah permintaan (kapasitas inventori) pada kasus perencanaan produksi.
2. Biaya transportasi per unit komoditas dari setiap daerah sumber menuju berbagai daerah tujuan pada kasus pendistribusian; biaya produksi dan inventori per unit pada kasus perencanaan produksi.
Karena hanya ada satu jenis komoditas, pada dasarnya setiap daerah tujuan dapat menerima komoditas dari sembarang daerah sumber, kecuali ada kendala lainnya. Kendala yang mungkin terjadi adalah tidak adanya jaringan transportasi dari suatu sumber menuju sutau tujuan; waktu pengangkutan yang lebih lama dibandingkan masa berlaku komoditas.
Meskipun demikian, metode transportasi tidak hanya berguna untuk optimasi pengangkutan komoditas (barang) dari daerah sumber menuju daerah tujuan. Metode transportasi juga dapat digunakan untuk perencanaan produksi. Data yang dibutuhkan dalam metode transportasi adalah:
1. Level suplai pada setiap daerah sumber dan level permintaan pada setiap daerah tujuan untuk kasus pendistribusian barang; jumlah produksi dan jumlah permintaan (kapasitas inventori) pada kasus perencanaan produksi.
2. Biaya transportasi per unit komoditas dari setiap daerah sumber menuju berbagai daerah tujuan pada kasus pendistribusian; biaya produksi dan inventori per unit pada kasus perencanaan produksi.
Karena hanya ada satu jenis komoditas, pada dasarnya setiap daerah tujuan dapat menerima komoditas dari sembarang daerah sumber, kecuali ada kendala lainnya. Kendala yang mungkin terjadi adalah tidak adanya jaringan transportasi dari suatu sumber menuju sutau tujuan; waktu pengangkutan yang lebih lama dibandingkan masa berlaku komoditas.
• ai (i=1, 2, 3, …, m) menunjukkan suplai pada sumber ke-i.
• bj (j=1, 2, 3, …, n) menunjukkan permintaan pada tujuan ke-j.
• cij menunjukkan biaya transportasi per unit dari sumber ke-i menuju tujuan-j.
• xij menunjukkan jumlah yang diangkut/dialokasikan dari sumber i menuju tujuan j.
Seperti yang telah disebutkan sebelumnya, metode transportasi tidak hanya digunakan dalam pendistribusian barang (komoditas). Metode transportasi juga dapat digunakan untuk mengoptimalkan sistem produksi. Persamaan elemen antara sistem transportasi dengan sistem produksi ditunjukkan tabel di bawah ini.
• bj (j=1, 2, 3, …, n) menunjukkan permintaan pada tujuan ke-j.
• cij menunjukkan biaya transportasi per unit dari sumber ke-i menuju tujuan-j.
• xij menunjukkan jumlah yang diangkut/dialokasikan dari sumber i menuju tujuan j.
Seperti yang telah disebutkan sebelumnya, metode transportasi tidak hanya digunakan dalam pendistribusian barang (komoditas). Metode transportasi juga dapat digunakan untuk mengoptimalkan sistem produksi. Persamaan elemen antara sistem transportasi dengan sistem produksi ditunjukkan tabel di bawah ini.
FORMULASI MATEMATIK
Karena tujuan optimasi adalah penentuan total biaya minimum, maka tujuan dalam model matematiknya adalah minimisasi. Alternatif keputusan dalam hal ini adalah penentuan jumlah yang akan diangkut dari daerah sumber i menuju tujuan j. Koefisien fungsi tujuan oleh karenanya adalah biaya angkut per unit dari sumber i menuju tujuan j. Kendala atau sumber daya yang membatasi penentuan total biaya transportasi optimum adalah jumlah suplai pada masing-masing daerah sumber dan jumlah permintaan pada masing-masing daerah tujuan.
Menggunakan xij sebagai jumlah yang diangkut dari sumber i menuju tujuan j, cij sebagai biaya transportasi per unit komoditas dari sumber i menuju tujuan j, ai sebagai jumlah suplai pada sumber i dan bj sebagai permintaan pada tujuan j, maka bentuk PL kasus transportasi adalah:
Karena tujuan optimasi adalah penentuan total biaya minimum, maka tujuan dalam model matematiknya adalah minimisasi. Alternatif keputusan dalam hal ini adalah penentuan jumlah yang akan diangkut dari daerah sumber i menuju tujuan j. Koefisien fungsi tujuan oleh karenanya adalah biaya angkut per unit dari sumber i menuju tujuan j. Kendala atau sumber daya yang membatasi penentuan total biaya transportasi optimum adalah jumlah suplai pada masing-masing daerah sumber dan jumlah permintaan pada masing-masing daerah tujuan.
Menggunakan xij sebagai jumlah yang diangkut dari sumber i menuju tujuan j, cij sebagai biaya transportasi per unit komoditas dari sumber i menuju tujuan j, ai sebagai jumlah suplai pada sumber i dan bj sebagai permintaan pada tujuan j, maka bentuk PL kasus transportasi adalah:
Min z = ΣΣ cijxij
Terhadap Σ xij ≤ ai, i = 1, 2, ..., m
Σ xij ≥ bj, j = 1, 2, ..., n
xij ≥ 0
Terhadap Σ xij ≤ ai, i = 1, 2, ..., m
Σ xij ≥ bj, j = 1, 2, ..., n
xij ≥ 0
Jika total suplai (Σ ai) sama dengan total permintaan (Σ bj), maka formulasi yang dihasilkan disebut sebagai model transportasi seimbang. Perbedaannya dengan formulasi di atas hanya pada penggunaan persamaan pada kendala, yaitu:
Σ xij = ai, i = 1, 2, ..., m
Σ xij = bj, j = 1, 2, ..., n
Σ xij = bj, j = 1, 2, ..., n
Algoritma penyelesaian metode transportasi yang akan dibahas di bawah digunakan untuk model transportasi seimbang.
PENENTUAN SOLUSI AWAL
Sama dengan algortima penyelesaian simpleks yang sudah dibahas sebelumnya, penyelesaian menggunakan metode transportasi juga dimulai dengan penentuan solusi awal. Penentuan solusi awal dapat dilakukan dengan memilih salah satu dari metode sudut barat laut, biaya terkecil atau Vogel’s Approximation Method (VAM). Solusi awal layak dilihat dari jumlah sel yang teralokasi. Solusi layak jika jumlah sel yang terisi sebanyak m + n -1 (m menunjukkan jumlah sumber dan n adalah jumlah tujuan).
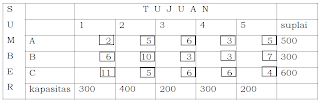
PT. XYZ mempunyai 3 pabrik yang berlokasi di 3 kota berbeda dan memproduksi minuman ringan yang dibotolkan. Produk dari ketiga pabrik didistribusikan ke 5 gudang yang terletak di lima kota daerah distribusi. Biaya pengangkutan per krat minuman (ratus rupiah), jumlah suplai pada masing-masing pabrik (dalam ribu krat) dan daya tampung pada masing-masing gudang (dalam ribu krat) setiap hari ditunjukkan tabel di bawah ini:
Biaya distribusi per unit dan kapasitas sumber dan tujuan.
Tabel TransportasiBERSAMBUNG............ hehehheeh




No comments:
Post a Comment
Komentar anda saya tunggu lho